Geometric Progression Sum to Infinity
The sum of the first four terms is 30 and all the. You can put this solution on.

Proof Of The Geometric Series Formula Finite Infinite Youtube
The sum in geometric progression also called geometric series is given by.

. I Show that the common ratio is. Ii Give e third term is 9 find the first term. Only when a certain condition is met will the infinite sum result in.
In this session we prove the formula for the sum to infinity of a convergent geometric series and apply itTimecodes 000 - Intro 008 - Objectives 019 - Re. Asymptote Limit of the tangent line at a point. Find step-by-step Geometry solutions and your answer to the following textbook question.
Solved examples to find. Learn the Concepts on. The sum of an infinite Geometric Progression with first term a and common ratio r -1 r 1 ie r 1 is S a1 - r Sum of an infinite Geometric Progression.
Sum to Infinity of an Arithmetic Geometric Series. The list of formulas related to GP is given below which will help in solving different. Simplify the equation obtained in step 4 by applying the formula for sum of geometric series.
Tutorial on Geometric series. The number of terms in infinite geometric progression will approach to infinity n. We will derive the formula in finding the sum of the terms of infinite geometric.
Up to 10 cash back The infinity symbol that placed above the sigma notation indicates that the series is infinite. An arithmetic-geometric progression AGP is a progression in which each term can be represented as the product of the terms of an arithmetic progressions AP and a geometric. In a geometric progression the sum to infinity is four times the first term.
This example uses simultaneous equationsDo you need more videos. To find the sum of the above infinite geometric series first check if the. Here we have studied the sum of infinite terms of the geometric series by using solved examples that will help understand the concept easily.
In this lesson we will go over how to determine the sum to infintiy of a geometric series. The sum to infinity of a geometric series is given by the formula Sa1 1-r where a1 is the first term in the series and r is found by dividing any term by the term immediately before it. It is given that a_0 frac 11-r 32 and a_0 frac 1-r51-r 31 Multiplying both sides of each equation by frac 1-r1-r.
This is called the geometric progression formula of sum to infinity. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. In this video we will discuss infinite geometric series or sum to infinity.
The sum ot infinity of a geometric progression is four times the first term find the common ratio Answer by ramkikk66644 Show Source. The infinite sum of an infinite geometric series formula is often infinity either positive or negative infinity. Answer 1 of 2.
Iii Find the sum of the first. We get a_0 32 - 32r for the first which we can. The sum to infinity of a geometric series is 32.
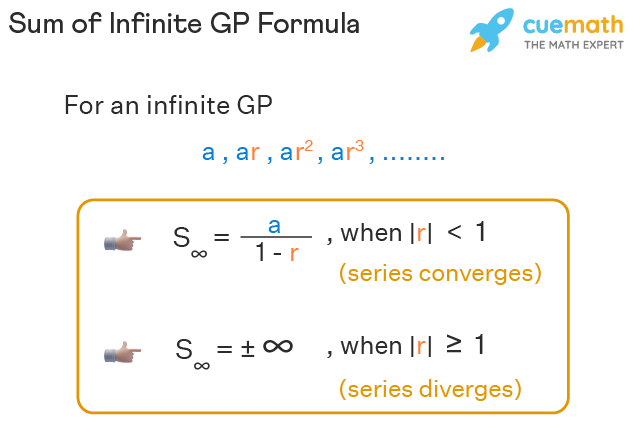
Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp

Geometric Series Sum To Infinity Examsolutions Youtube

Mathwords Infinite Geometric Series
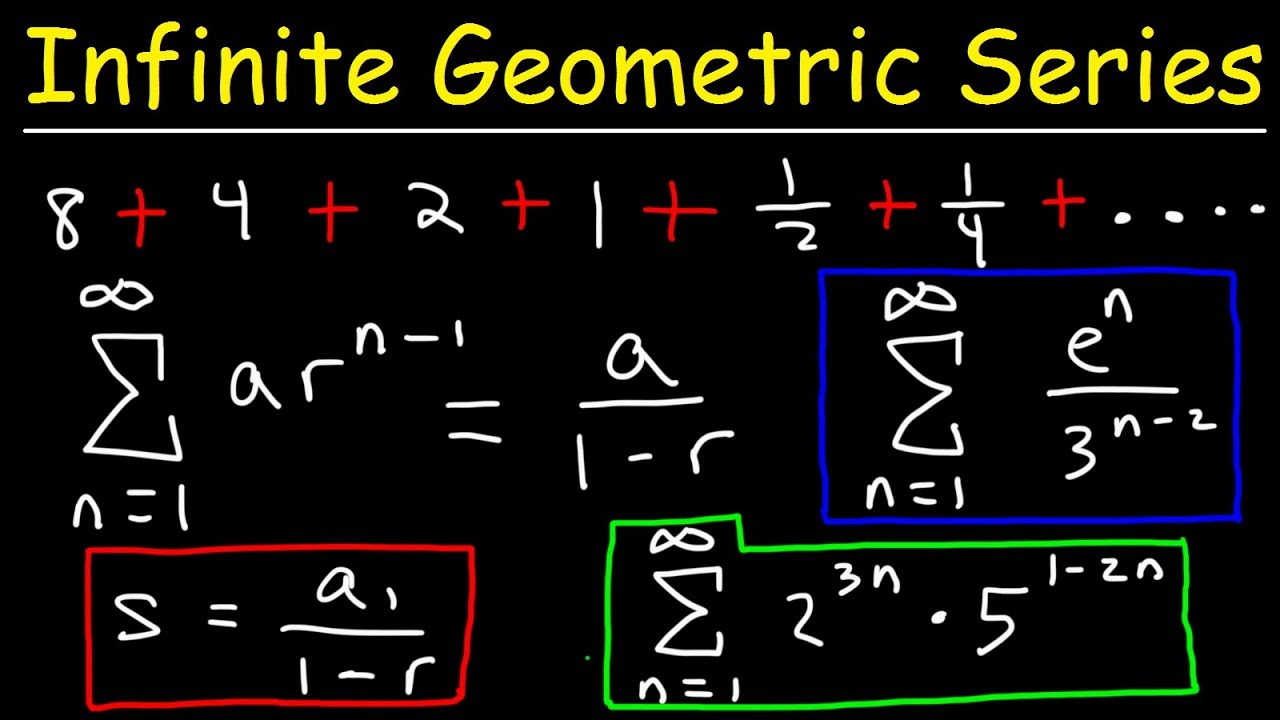
Finding The Sum Of An Infinite Geometric Series Youtube
0 Response to "Geometric Progression Sum to Infinity"
Post a Comment